Modelagem e Resolução do Problema do Caixeiro Viajante com Python e Pyomo

Feb 2020 8 minutos de leitura

Nessa publicação¹, abordaremos um dos mais famosos problemas da Pesquisa Operacional, o Problema do Caixeiro Viajante (PCV). O problema faz a seguinte pergunta:

Dado um conjunto de cidades e as distâncias entre cada par delas, qual é a rota mais curta (tour) que visita cada uma delas e retorna à cidade de origem?

Uma formulação por meio de programação linear inteira

O PCV pode ser formulado como um modelo de programação linear inteira (PLI). A seguir, desenvolvemos a bem conhecida formulação Miller-Tucker-Zemlin (MTZ). Embora não seja a mais eficiente computacionalmente, é uma das mais fácéis de codificar.

Rotule as cidades como $1,…, n$, em que $n$ é o número total de cidades e arbitrariamente assuma 1 como a origem. Defina as variáveis de decisão:

$$ x_{ij} = \begin{cases} & 1 \quad \text{ se a rota incluir um link direto entre cidades } i \text{ e } j, \\
& 0 \quad \text{ caso contrário}. \end{cases} $$

Além disso, para cada cidade $i = 1, 2, …, n$, seja $u_i \in \mathbb {R} ^ +$ uma variável auxiliar e seja $c_ {ij}$ a distância entre as cidades $i$ e $j$. Em seguida, a formulação de MTZ para o PCV é a seguinte:

$$ \begin{align} \text{min} \quad & \sum_{i = 1}^{n} \sum_{j = 1, j \neq i}^{n} c_{ij} x_{ij}, \\
\text{sujeito a} \\
& \sum_{i=1, i \neq j}^{n} x_{ij} = 1, \quad j=1,2,…,n,\\
& \sum_{j=1, j \neq i}^{n} x_{ij} = 1, \quad i=1,2,…,n,\\
& u_i - u_j + n x_{ij} \leq n-1, \quad 2 \leq i \neq j \leq n, \\
& x_{ij} \in \{0,1\} \quad i, j =1,2,…,n, \quad i \neq j, \\
& u_i \in \mathbb{R}^+ \quad i=1,2,…,n. \\
\end{align} $$ Na formulação acima, observe que o primeiro conjunto de igualdades requer que cada cidade receba 1 link de exatamente outra cidade, e o segundo conjunto de igualdades exige que de cada cidade saia 1 link para exatamente uma próxima cidade.

Observe que essas restrições não garantem a formação de uma única rota abrangendo todas as cidades, já que elas permitem a formação de subrotas (ciclos). Para excluir soluções que contém subrotas, o terceiro conjunto de restrições é necessário. Ele é conhecido como restrições de eliminação de subrotas de MTZ.

Introduzindo o Pyomo

Para resolver o PCV, usaremos o Pyomo, que é uma linguagem de modelagem de otimização de código-fonte aberto baseada em Python. Se você já teve experiência com qualquer linguagem de programação (especialmente Python), modelar e resolver um problema com o Pyomo será uma tarefa simples.

O Pyomo permite escolher entre uma variedade de solvers de programação linear inteira, de código aberto e comercial. Nessa publicação, faremos uso do CPLEX IBM Solver para resolver a formulação MTZ do PCV. Você pode usar qualquer outro solver de PLI suportado pelo Pyomo.

Leitura dos Dados

O primeiro passo é inserir os dados, ou seja, fornecer uma matriz de distâncias (ou matriz de custos), que fornece as distâncias entre os pares de cidades.

Para fins pedagógicos e práticos, usaremos uma matriz de custos com $n = 17$ cidades ( clique aqui para baixar o arquivo ).

O arquivo pode ser lido em Python da seguinte maneira:

file = open('17.txt')
lines = file.readlines()
file.close()

for i in range(len(lines)):
    aux = lines[i][:-1].split('\t')
    aux = [int(i) for i in aux if i!= '']
    cost_matrix.append(aux)

n = len(cost_matrix)

As variáveis cost_matrix e n contêm a matriz de custos e o número de cidades, respectivamente. Agora poderemos usar esses elementos para definir as restrições.

Construção do Modelo

Para usar o Pyomo e resolver o problema, precisamos fazer um único import:

import pyomo.environ as pyEnv

Agora podemos inicializar o modelo:

#Model
model = pyEnv.ConcreteModel()

#Indexes for the cities
model.M = pyEnv.RangeSet(n)                
model.N = pyEnv.RangeSet(n)

#Index for the dummy variable u
model.U = pyEnv.RangeSet(2,n)

onde

ConcreteModel() cria o modelo;
RangeSet(n) cria um índice de 1 a n;
RangeSet(2,n) cria um índice de 2 a n;

Variáveis de Decisão

As variáveis de decisão são declaradas da seguinte maneira:

#Decision variables xij
model.x = pyEnv.Var(model.N,model.M, within=pyEnv.Binary)

#Dummy variable ui
model.u = pyEnv.Var(model.N, within=pyEnv.NonNegativeIntegers,bounds=(0,n-1))

onde

Var(model.N,model.M, within=pyEnv.Binary) cria $n$ variáveis de decisão binárias de tamanho $m$ cada uma;
Var(model.N, within=pyEnv.NonNegativeIntegers,bounds=(0,n-1)) cria $n$ variáveis de decisão inteiras não-negativas que só podem assumir valores entre 0 e $n-1$.

Matriz de Custos

Em seguida, devemos fornecer ao modelo a matriz de custos:

#Cost Matrix cij
model.c = pyEnv.Param(model.N, model.M,initialize=lambda model, i, j: cost_matrix[i-1][j-1])

onde Param(modelo.N, model.M,initialize=lambda model, i, j: cost_matrix[i-1][j-1]) fornece um parâmetro $n \times m$ para o modelo usando uma função lambda.

Função Objetivo

Depois de definir todas as variáveis de decisão e fornecer os parâmetros, podemos declarar a função objetivo:

def obj_func(model):
    return sum(model.x[i,j] * model.c[i,j] for i in model.N for j in model.M)

model.objective = pyEnv.Objective(rule=obj_func,sense=pyEnv.minimize)

Primeiro, definimos uma função que retorna nossa função objetivo. Observe que usamos a técnica list comprehension, se você não está familiarizado com ela, essa página tem um tutorial muito bom.

Objective(rule=obj_func,sense=pyEnv.minimize) cria a função objetivo do modelo e define sua direção de otimização (maximizar ou minimizar). No PCV, queremos minimizar o custo total, ou seja, definimos sense=pyEnv.minimize.

Restrições

As restrições são declaradas de maneira muito semelhante à função objetivo. O primeiro conjunto de restrições, que requer que cada cidade receba 1 link de exatamente outra cidade, pode ser formulado da seguinte maneira:

def rule_const1(model,M):
    return sum(model.x[i,M] for i in model.N if i!=M ) == 1

model.const1 = pyEnv.Constraint(model.M,rule=rule_const1)

onde Constraint(model.M,rule=rule_const1) cria $m$ restrições definidas por rule_const1.

O segundo conjunto de igualdades que exige que, de cada cidade saia 1 link para exatamente uma próxima cidade, pode ser formulado da seguinte maneira:

def rule_const2(model,N):
    return sum(model.x[N,j] for j in model.M if j!=N) == 1

model.rest2 = pyEnv.Constraint(model.N,rule=rule_const2)

onde Constraint(model.N,rule=rule_const2)cria $n$ restrições definidas por rule_const2.

O terceiro e último conjunto de restrições corresponde às restrições de eliminação de subtours MTZ:

def rule_const3(model,i,j):
    if i!=j: 
        return model.u[i] - model.u[j] + model.x[i,j] * n <= n-1
    else:
        #Yeah, this else doesn't say anything
        return model.u[i] - model.u[i] == 0 
    
model.rest3 = pyEnv.Constraint(model.U,model.N,rule=rule_const3)

onde Constraint(model.U,Model.N,rule=rule_const3) cria $u \times n$ restrições definidas por rule_const3.

Uma função do tipo rule deve retornar um objeto Pyomo, por isso que tivemos que escrever aquele else estranho.

Finalmente, podemos imprimir o modelo inteiro na tela chamando:

#Prints the entire model
model.pprint()

em que pprint () imprime o modelo inteiro (pode não ser uma boa ideia se o modelo for muito grande). Como alternativa, podemos usarpprint(filename=’file.txt’) para imprimir o modelo em um arquivo específico.

Resolvendo o Modelo

Para resolver o modelo, precisamos ter um solver já instalado, dado que o Pyomo é apenas uma linguagem de modelagem. Vamos usar o amplamente conhecido solver IBM CPLEX, mas você pode usar muitos outros comerciais e não comerciais solvers, como Gurobi, GLPK, CBC, etc.

O código a seguir cria uma instância do solver e, em seguida, resolve o modelo:

#Solves
solver = pyEnv.SolverFactory('cplex')
result = solver.solve(model,tee = False)

#Prints the results
print(result)

onde SolverFactory(‘cplex’) cria uma instância do solver; solve(model, tee= False) resolve o modelo;

Usando tee = False as mensagens de log do solver são desativadas. Para habilitá-las, basta definir tee= True.

A figura abaixo mostra os resultados retornados pelo solver:

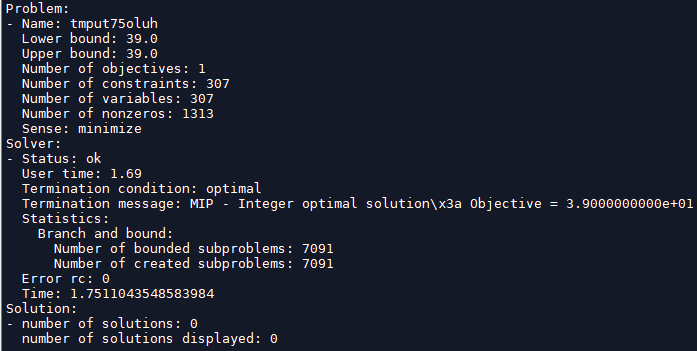
Para ver os valores das variáveis de decisão, podemos fazer o seguinte:

l = list(model.x.keys())
for i in l:
    if model.x[i]() != 0:
        print(i,'--', model.x[i]())

A figura abaixo mostra apenas as variáveis onde $x_{ij} = 1$.

Variables for which $x_{ij} = 1$ in the optimal tour.

Assim concluímos que, a tour ótima a partir da cidade 1 é $$ \begin{align} & 1 \to 17 \to 8 \to 9 \to 4 \to 5 \to 15 \to 7 \to 16 \to 6 \to \\
& \to 13 \to 10 \to 11 \to 2 \to 14 \to 3 \to 12 \to 1 \end{align} $$

Na prática

O PCV é um problema NP-hard amplamente estudado. O número de tours possíveis aumenta fatorialmente a partir do número de cidades. A formulação MTZ não consegue obter soluções ótimas em instâncias grandes dentro de tempos aceitáveis, a relaxação linear é muito fraca. Existem abordagens alternativas que podem obter soluções ótimas ou muito boas para grandes instâncias. Concorde é um algoritmo exato baseado no Método de plano de corte de Dantzig onde uma tour ótima para uma instância com 85900 cidades foi obtida com sucesso. Alternativamente, tours muito boas podem ser obtidas usando heurísticas como LKH ou simulated annealing.

Portanto, o PCV é considerado um problema resolvido na prática. Contudo, a classe mais geral de problemas de roteamento de veículos (PRV), que incluem outras restrições ausentes no TSP clássico, está longe de ser satisfatoriamente resolvido. Para citar algumas restrições encontradas em problemas reais, dentre as várias possíveis: vários veículos com capacidade limitada, vários depósitos, janelas de tempo, cargas fracionárias, demandas estocásticas e frotas heterogêneas. A combinação dessas restrições dá origem a diferentes problemas com diferentes graus de dificuldade.

Extras

Para encontrar mais exemplos do Pyomo, acesse a Página do GitHub deles. Além disso, você pode encontrar um manual em português de Pyomo no meu GitHub .

Para citar este artigo (bibtex)

@misc{woche,
  author="Woche, Claudemir",
  title="Modelagem e Resolução do Problema do Caixeiro Viajante com Python e Pyomo",
  year=2020,
  url=http://www.opl.ufc.br/pt/post/tsp/,
  note = "[Online; accessed 2021-05-07]"
}

Este post é uma adaptação de um artigo publicado originalmente no Medium. ↩︎