O Problema de Máquina Única para Minimização do Atraso Total
Problemas de programação da produção possuem diversas aplicações industriais, notadamente na gestão de operações e prestação de serviços. Existem diversos modelos de ambientes de produção que podem representar situações encontradas no mundo real. Dentre estes, se destaca o ambiente de máquina única, por sua importância teórica e prática. É oportuno destacar que todos os ambientes de produção podem ser reduzidos ao ambiente de máquina única, se existe apenas uma máquina disponível.
No ambiente de máquina única, existe um conjunto de trabalhos a ser processado em uma única máquina. Cada trabalho necessariamente deve ter um tempo de processamento associado à máquina em análise. Eventualmente, outras características também podem ser associadas aos trabalhos, tais como prazos de entrega, tempos de preparação das máquinas dependentes da sequência de produção ou o consumo de recursos.
Sejam $n$ trabalhos a serem processados na máquina única, cada qual com um tempo de processamento associado, existem $n!$ sequências possíveis. De acordo com a sequência estipulada, é possível calcular o tempo de término de cada um os trabalhos dado por $C = \{C_1, C_2,…, C_n\}$. Dependendo da função objetivo em análise, o problema pode ser resolvido de forma exata por um algoritmo polinomial ou então pertencer à classe de problemas NP-difícil.
Se a função objetivo para o problema em estudo é a minimização do tempo de finalização do projeto, usualmente conhecido como makespan ($C_{max}$), temos que:
$$C_{max} = max \{C\}$$
Ou seja, o makespan é o maior tempo de finalização dentre todas as tarefas. No que se refere ao ambiente de máquina única, caso não sejam consideradas restrições adicionais, é possível observar que todas as sequências apresentam o mesmo makespan. Desta forma, o problema 1||$C_{max}$ apresenta solução trivial.
Nesse tutorial, será abordado o problema 1||$\Sigma T_j$, o qual é NP-difícil. Primeiramente, um modelo de programação linear inteira é apresentado. Em seguida, sua implementação na linguagem de programação Julia é descrita.
Sejam $n$ trabalhos a serem processados em uma máquina única, cada qual com um tempo de processamento $p_i$ e um prazo de entrega $d_i$, cada trabalho processado na posição $j$ da sequência possui um tempo de término $C_j$ e um atraso $T_j$. O objetivo do problema é determinar uma sequência de produção que apresente o menor somatório dos atrasos possível.
Visto que o problema em estudo é pertencente à classe NP-difícil, modelos de programação linear inteira são de grande valia para sua resolução, notadamente para instâncias de pequeno e médio porte. A formulação apresentada aqui é baseada em variáveis posicionais, as quais irão determinar a posição de um dado trabalho na sequencia de produção. É apresentada a seguir a notação da formulação matemática, baseada no modelo proposto por Della Croce et al. (2014).
Índices e conjuntos
$i$: índice para os trabalhos {1,2,…,$n$}.
$j$: índice para as posições {1,2,…,$n$}.
Parâmetros
$p_{i}$: tempo de processamento do trabalho $i$.
$d_{i}$: prazo de entrega do trabalho $i$.
Variáveis de decisão
$T_{j}$: atraso associado ao trabalho processado na posição $j$.
$C_{j}$: tempo de término do trabalho processado na posição $j$.
$$
x_{ij} =
\begin{cases}
& 1, \mbox{ se o trabalho $i$ é processado na posição $j$ da sequência.} \\
& 0, \mbox{ caso contrário}
\end{cases}
$$
O modelo de programação linear inteira para o problema em estudo é
descrito a seguir.
$$
\begin{align}
\text{minimizar} \quad & \nonumber\\
& \sum_{j=1}^{n} T_{j} \label{fo}\tag{1}\\
\text{sujeito a} \quad & \nonumber\\
& \sum_{i=1}^{n} x_{ij} = 1, \quad \forall j \label{r1}\tag{2}\\
& \sum_{j=1}^{n} x_{ij} = 1, \quad \forall i \label{r2}\tag{3}\\
& C_1 = \sum_{i=1}^{n} p_{i}x_{i1} \label{r3}\tag{4}\\
& C_{j} \geq C_{j-1} + \sum_{i=1}^{n} p_{i}x_{ij}, \quad \forall j \in \{2,…,n\} \label{r4}\tag{5}\\
& T_{j} \geq C_{j} + \sum_{i=1}^{n} d_{i}x_{ij}, \quad \forall j \label{r5}\tag{6}\\
& T_{j} \geq 0, \quad \forall j \label{r6}\tag{7}\\
& C_{j} \geq 0, \quad \forall j \label{r7}\tag{8}\\
& x_{ij} \in \{0,1\}, \quad \forall i, j \label{r8}\tag{9}
\end{align}
$$
A função objetivo \eqref{fo} corresponde à minimização do atraso total. O conjunto de restrições do tipo \eqref{r1} garante que cada trabalho é alocado a apenas uma posição da sequência e o conjunto de restrições do tipo \eqref{r2} garante que cada posição recebe apenas um trabalho. Estes dois conjuntos de restrições garantem que a solução do problema é uma permutação dos trabalhos. A restrição \eqref{r3} determina o tempo de término do trabalho alocado na primeira posição da sequência. O conjunto de restrições do tipo \eqref{r4} determina o tempo de término dos trabalhos processados nas posições subsequentes da sequência. O conjunto de restrições do tipo \eqref{r5} determina o atraso correspondente aos trabalhos processados em cada posição $j$ da sequência. Finalmente, os conjuntos de restrições \eqref{r6}, \eqref{r7} , e \eqref{r8} definem o escopo das variáveis de decisão do modelo.
A seguir, é apresentada uma implementação do modelo de programação linear inteira proposto na linguagem Julia (https://julialang.org/). Para modelagem do problema, é utilizada a linguagem de modelagem JuMP ( https://julialang.org/ ), a qual deve ter sido previamente instalada pelo usuário. Como resolvedor, utilizamos o Cbc (https://github.com/coin-or/Cbc), por se tratar de um resolvedor gratuito e de código aberto. O leitor pode utilizar outro resolvedor para realização dos seus estudos, sem nenhum prejuízo em termos de conteúdo.
Na implementação apresentada, é criada uma função denominada “single” que possui dois argumentos: um vetor de tempos de processamento e um vetor de prazos de entrega. A partir do tamanho destes vetores, é possível determinar o número de trabalhos através do comando “length”. Um objeto denominado “model” é criado para receber variáveis, restrições e permitir a manipulação do modelo desenvolvido.
Após a criação do objeto para representação do modelo, devem ser declaradas as variáveis, função objetivo e restrições do problema. No código a seguir, representamos as Equações (2) - (8) por meio da sintaxe da linguagem de modelagem JuMP.
Para solucionar o problema, deve chamada a função “optimize!”. Foram criadas duas variáveis para armazenar o valor da solução ótima, bem como o tempo computacional necessário para a resolução do modelo (denominadas respectivamente de zIP e tzIP).
using JuMP, Cbc
function single(p, d)
N = length(p)
model = Model(optimizer_with_attributes(Cbc.Optimizer))
# Decision variables
@variable(model,T[j in 1:N]>=0)
@variable(model,C[j in 1:N]>=0)
@variable(model,x[i in 1:N, j in 1:N],Bin)
# Objective function
@objective(model, Min, sum(T[j] for j in 1:N))
# Constraints
@constraint(model,[j in 1:N], sum(x[i,j] for i in 1:N) == 1)
@constraint(model,[i in 1:N], sum(x[i,j] for j in 1:N) == 1)
@constraint(model,C[1] == sum(p[i] * x[i,1] for i in 1:N))
@constraint(model,[j in 2:N], C[j] >= C[j-1] + sum(p[i] * x[i,j] for i in 1:N))
@constraint(model,[j in 1:N], T[j] >= C[j] - sum(x[i,j] * d[i] for i in 1:N))
# Build the model
optimize!(model)
zIP = objective_value(model)
tzIP = MOI.get(model, MOI.SolveTime())
return(zIP, tzIP)
end
A seguir, é ilustrada a aplicação do modelo, com base no exemplo apresentado por Arenales et al. (2006, p. 217). Neste exemplo, tem-se um conjunto de 8 trabalhos com tempos de processamento e prazos de entrega respectivamente dados por $p$ = {64, 53, 63, 99, 189, 44, 50, 22} e $d$ ={100, 70, 150, 601, 118, 590, 107, 180}.
Foi criado um arquivo “main.jl” no qual incluímos a função “single.jl” apresentada anteriormente. Foram criados dois vetores com os valores dos tempos de processamento e prazos de entrega, os quais foram utilizados como dados de entrada da função desenvolvida. A solução ótima global corresponde a um atraso total de 499 unidades de tempo, sendo obtida em um tempo computacional negligenciável (inferior à 1 segundo).
include("single.jl")
p = [64 53 63 99 189 44 50 22]
d = [100 70 150 601 118 590 107 180]
zIP, tzIP = single(p,d)
println("Optimal solution: ", zIP)
println("Computatonal time (s): ", tzIP)
Caso seja necessário determinar qual a sequência ótima de produção, é possível armazenar os valores da variável de decisão $x_{ij}$ obtidas pelo resolvedor por meio do comando:
x_val = value.(x)
No caso em questão, a solução obtida para a instância analisada foi a permutação $\pi$ ={2, 7, 3, 8, 1, 5, 6, 4}. A seguir, na Figura 1 abaixo é ilustrado o gráfico de Gantt com a solução ótima do problema.
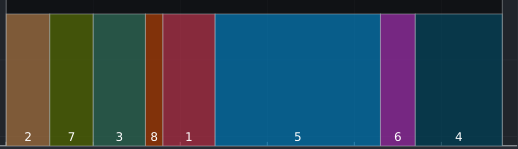
Para instâncias com dezenas ou centenas de trabalhos, os resolvedores geralmente conseguem obter soluções ótimas, utilizando o modelo proposto, em tempos computacionais admissíveis. Para instâncias com milhares de trabalhos, os resolvedores, em geral, passam a ter uma maior dificuldade em solucionar o modelo proposto, em tempo computacional aceitável.
Bibliografia consultada
-
Arenales, M., Armentano, V., Morabito, R., & Yanasse, H. (2006). Pesquisa Operacional para Cursos de Engenharia. 1a Edição. Editora Campus-Elsevier, Rio de Janeiro.
-
Della Croce, F., Salassa, F., & T’kindt, V. (2014). A hybrid heuristic approach for single machine scheduling with release times. Computers & Operations Research, 45, 7-11.
-
Du, J., & Leung, J. Y. T. (1990). Minimizing total tardiness on one machine is NP-hard. Mathematics of operations research, 15(3), 483-495.
-
Dunning, I., Huchette, J., & Lubin, M. (2017). JuMP: A modeling language for mathematical optimization. SIAM review, 59(2), 295-320.
-
Framinan, J. M., Leisten, R., & García, R. R. (2014). Manufacturing scheduling systems. An integrated view on Models, Methods and Tools, 51-63.
-
Michael, L. P. (2018). Scheduling: theory, algorithms, and systems. Springer.
Para citar este artigo (bibtex)
@misc{baprata,
author="Prata, Bruno de Athayde",
title="O Problema de Máquina Única para Minimização do Atraso Total",
year=2021,
url=http://www.opl.ufc.br/pt/post/single_machine_scheduling/,
note = "[Online; accessed 2021-05-07]"
}